LAPACK in your web browser: high-performance linear algebra with stdlib
Published December 20, 2024
pranavchiku
Pranav Goswami
Web applications are rapidly emerging as a new frontier for high-performance scientific computation and AI-enabled end-user experiences. Underpinning the ML/AI revolution is linear algebra, a branch of mathematics concerning linear equations and their representations in vector spaces and via matrices. LAPACK ("Linear Algebra Package") is a fundamental software library for numerical linear algebra, providing robust, battle-tested implementations of common matrix operations. Despite LAPACK being a foundational component of most numerical computing programming languages and libraries, a comprehensive, high-quality LAPACK implementation tailored to the unique constraints of the web has yet to materialize. That is...until now.
Hi! I am Pranav Goswami, and, over the past summer, I worked with Athan Reines to add initial LAPACK support to stdlib, a fundamental library for scientific computation written in C and JavaScript and optimized for use in web browsers and other web-native environments, such as Node.js and Deno. In this blog post, I'll discuss my journey, some expected and unexpected (!) challenges, and the road ahead. My hope is that this work, with a little bit of luck, provides a critical building block in making web browsers a first-class environment for numerical computation and machine learning and portends a future of more powerful AI-enabled web applications.
Sound interesting? Let's go!
What is stdlib?
Readers of this blog are likely Python enthusiasts and industry practitioners who are "in the know" regarding all things NumPy, SciPy, and PyTorch, but you may not be as intimately familiar with the wild world of web technologies. For those coming from the world of scientific Python, the easiest way to think of stdlib is as an open source scientific computing library in the mold of NumPy and SciPy. It provides multi-dimensional array data structures and associated routines for mathematics, statistics, and linear algebra, but uses JavaScript, rather than Python, as its primary scripting language. As such, stdlib is laser-focused on the web ecosystem and its application development paradigms. This focus necessitates some interesting design and project architecture decisions, which make stdlib rather unique when compared to more traditional libraries designed for numerical computation.
To take NumPy as an example, NumPy is a single monolithic library, where all of its components, outside of optional third-party dependencies such as OpenBLAS, form a single, indivisible unit. One cannot simply install NumPy routines for array manipulation without installing all of NumPy. If you are deploying an application which only needs NumPy's ndarray object and a couple of its manipulation routines, installing and bundling all of NumPy means including a considerable amount of "dead code". In web development parlance, we'd say that NumPy is not "tree shakeable". For a normal NumPy installation, this implies at least 30MB of disk space, and at least 15MB of disk space for a customized build which excludes all debug statements. For SciPy, those numbers can balloon to 130MB and 50MB, respectively. Needless to say, shipping a 15MB library in a web application for just a few functions is a non-starter, especially for developers needing to deploy web applications to devices with poor network connectivity or memory constraints.
Given the unique constraints of web application development, stdlib takes a bottom-up approach to its design, where every unit of functionality can be installed and consumed independently of unrelated and unused parts of the codebase. By embracing a decomposable software architecture and radical modularity, stdlib offers users the ability to install and use exactly what they need, with little-to-no excess code beyond a desired set of APIs and their explicit dependencies, thus ensuring smaller memory footprints, bundle sizes, and faster deployment.
As an example, suppose you are working with two stacks of matrices (i.e., two-dimensional slices of three-dimensional cubes), and you want to select every other slice and perform the common BLAS operation y += a * x, where x and y are ndarrays and a is a scalar constant. To do this with NumPy, you'd first install all of NumPy
pip install numpy
and then perform the various operations
# Import all of NumPy:import numpy as np# Define arrays:x = np.asarray(...)y = np.asarray(...)# Perform operation:y[::2,:,:] += 5.0 * x[::2,:,:]
With stdlib, in addition to having the ability to install the project as a monolithic library, you can install the various units of functionality as separate packages
npm install @stdlib/ndarray-fancy @stdlib/blas-daxpy
and then perform the various operations
// Individually import desired functionality:import FancyArray from '@stdlib/ndarray-fancy';import daxpy from '@stdlib/blas-daxpy';// Define ndarray meta data:const shape = [4, 4, 4];const strides = [...];const offset = 0;// Define arrays using a "lower-level" fancy array constructor:const x = new FancyArray('float64', [...], shape, strides, offset, 'row-major');const y = new FancyArray('float64', [...], shape, strides, offset, 'row-major');// Perform operation:daxpy(5.0, x['::2,:,:'], y['::2,:,:']);
Importantly, not only can you independently install any one of stdlib's over 4,000 packages, but you can also fix, improve, and remix any one of those packages by forking an associated GitHub repository (e.g., see @stdlib/ndarray-fancy). By defining explicit layers of abstraction and dependency trees, stdlib offers you the freedom to choose the right layer of abstraction for your application. In some ways, it's a simple—and, if you're accustomed to conventional scientific software library design, perhaps unorthodox—idea, but, when tightly integrated with the web platform, it has powerful consequences and creates exciting new possibilities!
What about WebAssembly?
Okay, so maybe your interest has piqued; stdlib seems intriguing. But what does this have to do with LAPACK in web browsers? Well, the goal of my summer project was to apply the stdlib ethos—small, narrowly scoped packages which do one thing and do one thing well—in bringing LAPACK to the web.
But wait, you say! That is an extreme undertaking. LAPACK is vast, with approximately 1,700 routines, and implementing even 10% of them within a three-month time frame is a significant challenge. Wouldn't it be better to just compile LAPACK to WebAssembly, a portable compilation target for programming languages such as C, Go, and Rust, which enables deployment on the web, and call it a day?
Unfortunately, there are several issues with this approach.
- Compiling Fortran to WebAssembly is still an area of active development (see 1, 2, 3, 4, and 5). At the time of this post, a common approach is to use
f2cto compile Fortran to C and then to perform a separate compilation step to convert C to WebAssembly. However, this approach is problematic asf2conly fully supports Fortran 77, and the generated code requires extensive patching. Work is underway to develop an LLVM-based Fortran compiler, but gaps and complex toolchains remain. - As alluded to above in the discussion concerning monolithic libraries in web applications, the vastness of LAPACK is part of the problem. Even if the compilation problem is solved, including a single WebAssembly binary containing all of LAPACK in a web application needing to use only one or two LAPACK routines means considerable dead code, resulting in slower loading times and increased memory consumption.
- While one could attempt to compile individual LAPACK routines to standalone WebAssembly binaries, doing so could result in binary bloat, as multiple standalone binaries may contain duplicated code from common dependencies. To mitigate binary bloat, one could attempt to perform module splitting. In this scenario, one first factors out common dependencies into a standalone binary containing shared code and then generates separate binaries for individual APIs. While suitable in some cases, this can quickly get unwieldy, as this approach requires linking individual WebAssembly modules at load-time by stitching together the exports of one or more modules with the imports of one or more other modules. Not only can this be tedious, but this approach also entails a performance penalty due to the fact that, when WebAssembly routines call imported exports, they now must cross over into JavaScript, rather than remaining within WebAssembly. Sound complex? It is!
- Apart from WebAssembly modules operating exclusively on scalar input arguments (e.g., computing the sine of a single number), every WebAssembly module instance must be associated with WebAssembly memory, which is allocated in fixed increments of 64KiB (i.e., a "page"). And importantly, as of this blog post, WebAssembly memory can only grow and never shrink. As there is currently no mechanism for releasing memory to a host, a WebAssembly application's memory footprint can only increase. These two aspects combined increase the likelihood of allocating memory which is never used and the prevalence of memory leaks.
- Lastly, while powerful, WebAssembly entails a steeper learning curve and a more complex set of often rapidly evolving toolchains. In end-user applications, interfacing between JavaScript—a web-native dynamically-compiled programming language—and WebAssembly further brings increased complexity, especially when having to perform manual memory management.
To help illustrate the last point, let's return to the BLAS routine daxpy, which performs the operation y = a*x + y and where x and y are strided vectors and a a scalar constant. If implemented in C, a basic implementation might look like the following code snippet.
void c_daxpy(const int N, const double alpha, const double *X, const int strideX, double *Y, const int strideY) { int ix; int iy; int i; if (N <= 0) { return; } if (alpha == 0.0) { return; } if (strideX < 0) { ix = (1-N) * strideX; } else { ix = 0; } if (strideY < 0) { iy = (1-N) * strideY; } else { iy = 0; } for (i = 0; i < N; i++) { Y[iy] += alpha * X[ix]; ix += strideX; iy += strideY; } return;}
After compilation to WebAssembly and loading the WebAssembly binary into our web application, we need to perform a series of steps before we can call the c_daxpy routine from JavaScript. First, we need to instantiate a new WebAssembly module.
const binary = new UintArray([...]);const mod = new WebAssembly.Module(binary);
Next, we need to define module memory and create a new WebAssembly module instance.
// Initialize 10 pages of memory and allow growth to 100 pages:const mem = new WebAssembly.Memory({ 'initial': 10, // 640KiB, where each page is 64KiB 'maximum': 100 // 6.4MiB});// Create a new module instance:const instance = new WebAssembly.Instance(mod, { 'env': { 'memory': mem }});
After creating a module instance, we can now invoke the exported BLAS routine. However, if data is defined outside of module memory, we first need to copy that data to the memory instance and always do so in little-endian byte order.
// External data:const xdata = new Float64Array([...]);const ydata = new Float64Array([...]);// Specify a vector length:const N = 5;// Specify vector strides (in units of elements):const strideX = 2;const strideY = 4;// Define pointers (i.e., byte offsets) for storing two vectors:const xptr = 0;const yptr = N * 8; // 8 bytes per double// Create a DataView over module memory:const view = new DataView(mem.buffer);// Resolve the first indexed elements in both `xdata` and `ydata`:let offsetX = 0;if (strideX < 0) { offsetX = (1-N) * strideX;}let offsetY = 0;if (strideY < 0) { offsetY = (1-N) * strideY;}// Write data to the memory instance:for (let i = 0; i < N; i++) { view.setFloat64(xptr+(i*8), xdata[offsetX+(i*strideX)], true); view.setFloat64(yptr+(i*8), ydata[offsetY+(i*strideY)], true);}
Now that data is written to module memory, we can call the c_daxpy routine.
instance.exports.c_daxpy(N, 5.0, xptr, 1, yptr, 1);
And, finally, if we need to pass the results to a downstream library without support for WebAssembly memory "pointers" (i.e., byte offsets), such as D3, for visualization or further analysis, we need to copy data from module memory back to the original output array.
for (let i = 0; i < N; i++) { ydata[offsetY+(i*strideY)] = view.getFloat64(yptr+(i*8), true);}
That's a lot of work just to compute y = a*x + y. In contrast, compare to a plain JavaScript implementation, which might look like the following code snippet.
function daxpy(N, alpha, X, strideX, Y, strideY) { let ix; let iy; let i; if (N <= 0) { return; } if (alpha === 0.0) { return; } if (strideX < 0) { ix = (1-N) * strideX; } else { ix = 0; } if (strideY < 0) { iy = (1-N) * strideY; } else { iy = 0; } for (i = 0; i < N; i++) { Y[iy] += alpha * X[ix]; ix += strideX; iy += strideY; } return;}
With the JavaScript implementation, we can then directly call daxpy with our externally defined data without the data movement required in the WebAssembly example above.
daxpy(N, 5.0, xdata, 1, ydata, 1);
At least in this case, not only is the WebAssembly approach less ergonomic, but, as might be expected given the required data movement, there's a negative performance impact, as well, as demonstrated in the following figure.
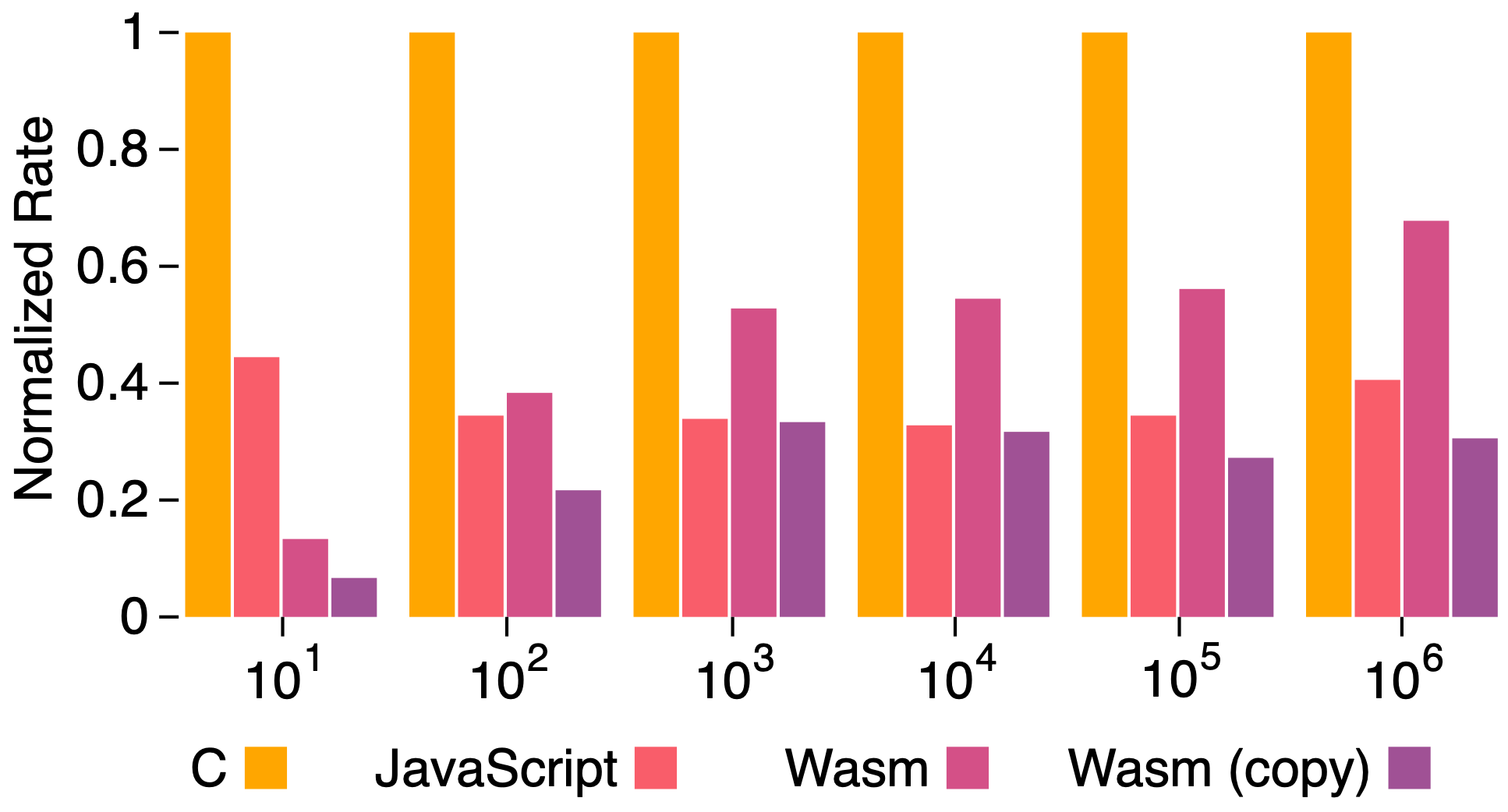
Figure 1: Performance comparison of stdlib's C, JavaScript, and WebAssembly (Wasm) implementations for the BLAS routine daxpy for increasing array lengths (x-axis). In the Wasm (copy) benchmark, input and output data is copied to and from Wasm memory, leading to poorer performance.
In the figure above, I'm displaying a performance comparison of stdlib's C, JavaScript, and WebAssembly (Wasm) implementations for the BLAS routine daxpy for increasing array lengths, as enumerated along the x-axis. The y-axis shows a normalized rate relative to a baseline C implementation. In the Wasm benchmark, input and output data is allocated and manipulated directly in WebAssembly module memory, and, in the Wasm (copy) benchmark, input and output data is copied to and from WebAssembly module memory, as discussed above. From the chart, we may observe the following:
- In general, thanks to highly optimized just-in-time (JIT) compilers, JavaScript code, when carefully written, can execute only 2-to-3 times slower than native code. This result is impressive for a loosely typed, dynamically compiled programming language and, at least for
daxpy, remains consistent across varying array lengths. - As data sizes and thus the amount of time spent in a WebAssembly module increase, WebAssembly can approach near-native (~1.5x) speed. This result aligns more generally with expected WebAssembly performance.
- While WebAssembly can achieve near-native speed, data movement requirements may adversely affect performance, as observed for
daxpy. In such cases, a well-crafted JavaScript implementation which avoids such requirements can achieve equal, if not better, performance, as is the case fordaxpy.
Overall, WebAssembly can offer performance improvements; however, the technology is not a silver bullet and needs to be used carefully in order to realize desired gains. And even when offering superior performance, such gains must be balanced against the costs of increased complexity, potentially larger bundle sizes, and more complex toolchains. For many applications, a plain JavaScript implementation will do just fine.
Radical modularity
Now that I've prosecuted the case against just compiling the entirety of LAPACK to WebAssembly and calling it a day, where does that leave us? Well, if we're going to embrace the stdlib ethos, it leaves us in need of radical modularity.
To embrace radical modularity is to recognize that what is best is highly contextual, and, depending on the needs and constraints of user applications, developers need the flexibility to pick the right abstraction. If a developer is writing a Node.js application, that may mean binding to hardware-optimized libraries, such as OpenBLAS, Intel MKL, or Apple Accelerate in order to achieve superior performance. If a developer is deploying a web application needing a small set of numerical routines, JavaScript is likely the right tool for the job. And if a developer is working on a large, resource intensive WebAssembly application (e.g., for image editing or a gaming engine), then being able to easily compile individual routines as part of the larger application will be paramount. In short, we want a radically modular LAPACK.
My mission during the Quansight internship was to lay the groundwork for such an endeavor, to work out the kinks and find the gaps, and to hopefully get us a few steps closer to high-performance linear algebra on the web. But what does radical modularity look like? It all begins with the fundamental unit of functionality, the package.
Every package in stdlib is its own standalone thing, containing co-localized tests, benchmarks, examples, documentation, build files, and associated meta data (including the enumeration of any dependencies) and defining a clear API surface with the outside world. In order to add LAPACK support to stdlib, that means creating a separate standalone package for each LAPACK routine with the following structure:
├── benchmark│ ├── c│ │ ├── Makefile│ │ └── benchmark.c│ ├── fortran│ │ ├── Makefile│ │ └── benchmark.f│ └── benchmark*.js├── docs│ ├── types│ │ ├── index.d.ts│ │ └── test.ts│ └── repl.txt├── examples│ ├── c│ │ ├── Makefile│ │ └── example.c│ └── index.js├── include/*├── lib│ ├── index.js│ └── *.js├── src│ ├── Makefile│ ├── addon.c│ ├── *.c│ └── *.f├── test│ └── test*.js├── binding.gyp├── include.gypi├── manifest.json├── package.json└── README.md
Briefly,
- benchmark: a folder containing micro-benchmarks to assess performance relative to a reference implementation (i.e., reference LAPACK).
- docs: a folder containing auxiliary documentation including REPL help text and TypeScript declarations defining typed API signatures.
- examples: a folder containing executable demonstration code, which, in addition to serving as documentation, helps developers sanity check implementation behavior.
- include: a folder containing C header files.
- lib: a folder containing JavaScript source implementations, with
index.jsserving as the package entry point and other*.jsfiles defining internal implementation modules. - src: a folder containing C and Fortran source implementations. Each modular LAPACK package should contain a slightly modified Fortran reference implementation (F77 to free-form Fortran). C files include a plain C implementation which follows the Fortran reference implementation, a wrapper for calling the Fortran reference implementation, a wrapper for calling hardware-optimized libraries (e.g., OpenBLAS) in server-side applications, and a native binding for calling into compiled C from JavaScript in Node.js or a compatible server-side JavaScript runtime.
- test: a folder containing unit tests for testing expected behavior in both JavaScript and native implementations. Tests for native implementations are written in JavaScript and leverage the native binding for interoperation between JavaScript and C/Fortran.
- binding.gyp/include.gypi: build files for compiling Node.js native add-ons, which provide a bridge between JavaScript and native code.
- manifest.json: a configuration file for stdlib's internal C and Fortran compiled source file package management.
- package.json: a file containing package meta data, including the enumeration of external package dependencies and a path to a plain JavaScript implementation for use in browser-based web applications.
- README.md: a file containing a package's primary documentation, which includes API signatures and examples for both JavaScript and C interfaces.
Given stdlib's demanding documentation and testing requirements, adding support for each routine is a decent amount of work, but the end result is robust, high-quality, and, most importantly, modular code suitable for serving as the foundation for scientific computation on the modern web. But enough with the preliminaries! Let's get down to business!
A multi-phase approach
Building on previous efforts which added BLAS support to stdlib, we decided to follow a similar multi-phase approach when adding LAPACK support in which we first prioritize JavaScript implementations and their associated testing and documentation and then, once tests and documentation are present, back fill C and Fortran implementations and any associated native bindings to hardware-optimized libraries. This approach allows us to put some early points on the board, so to speak, quickly getting APIs in front of users, establishing robust test procedures and benchmarks, and investigating potential avenues for tooling and automation before diving into the weeds of build toolchains and performance optimizations. But where to even begin?
To determine which LAPACK routines to target first, I parsed LAPACK's Fortran source code to generate a call graph. This allowed me to infer the dependency tree for each LAPACK routine. With the graph in hand, I then performed a topological sort, thus helping me identify routines without dependencies and which will inevitably be building blocks for other routines. While a depth-first approach in which I picked a particular high-level routine and worked backward would enable me to land a specific feature, such an approach might cause me to get bogged down trying to implement routines of increasing complexity. By focusing on the "leaves" of the graph, I could prioritize commonly used routines (i.e., routines with high indegrees) and thus maximize my impact by unlocking the ability to deliver multiple higher-level routines either later in my internship or by other contributors.
With my plan in hand, I was excited to get to work. For my first routine, I chose dlaswp, which performs a series of row interchanges on a general rectangular matrix according to a provided list of pivot indices and which is a key building block for LAPACK's LU decomposition routines. And that is when my challenges began...
Challenges
Legacy Fortran
Prior to my internship, I was (and still am!) a regular contributor to LFortran, a modern interactive Fortran compiler built on top of LLVM, and I was feeling fairly confident in my Fortran skills. However, one of my first challenges was simply understanding what is now considered "legacy" Fortran code. I highlight three initial hurdles below.
Formatting
LAPACK was originally written in FORTRAN 77 (F77). While the library was moved to Fortran 90 in version 3.2 (2008), legacy conventions still persist in the reference implementation. One of the most visible of those conventions is formatting.
Developers writing F77 programs did so using a fixed form layout inherited from punched cards. This layout had strict requirements concerning the use of character columns:
- Comments occupying an entire line must begin with a special character (e.g.,
*,!, orC) in the first column. - For non-comment lines, 1) the first five columns must be blank or contain a numeric label, 2) column six is reserved for continuation characters, 3) executable statements must begin at column seven, and 4) any code beyond column 72 was ignored.
Fortran 90 introduced the free form layout which removed column and line length restrictions and settled on ! as the comment character. The following code snippet shows the reference implementation for the LAPACK routine dlacpy:
SUBROUTINE dlacpy( UPLO, M, N, A, LDA, B, LDB )** -- LAPACK auxiliary routine --* -- LAPACK is a software package provided by Univ. of Tennessee, --* -- Univ. of California Berkeley, Univ. of Colorado Denver and NAG Ltd..--** .. Scalar Arguments .. CHARACTER UPLO INTEGER LDA, LDB, M, N* ..* .. Array Arguments .. DOUBLE PRECISION A( LDA, * ), B( LDB, * )* ..** =====================================================================** .. Local Scalars .. INTEGER I, J* ..* .. External Functions .. LOGICAL LSAME EXTERNAL lsame* ..* .. Intrinsic Functions .. INTRINSIC min* ..* .. Executable Statements ..* IF( lsame( uplo, 'U' ) ) THEN DO 20 j = 1, n DO 10 i = 1, min( j, m ) b( i, j ) = a( i, j ) 10 CONTINUE 20 CONTINUE ELSE IF( lsame( uplo, 'L' ) ) THEN DO 40 j = 1, n DO 30 i = j, m b( i, j ) = a( i, j ) 30 CONTINUE 40 CONTINUE ELSE DO 60 j = 1, n DO 50 i = 1, m b( i, j ) = a( i, j ) 50 CONTINUE 60 CONTINUE END IF RETURN** End of DLACPY* END
The next code snippet shows the same routine, but implemented using the free form layout introduced in Fortran 90.
subroutine dlacpy( uplo, M, N, A, LDA, B, LDB ) implicit none ! .. ! Scalar arguments: character :: uplo integer :: LDA, LDB, M, N ! .. ! Array arguments: double precision :: A( LDA, * ), B( LDB, * ) ! .. ! Local scalars: integer :: i, j ! .. ! External functions: logical LSAME external lsame ! .. ! Intrinsic functions: intrinsic min ! .. if ( lsame( uplo, 'U' ) ) then do j = 1, n do i = 1, min( j, m ) b( i, j ) = a( i, j ) end do end do else if( lsame( uplo, 'L' ) ) then do j = 1, n do i = j, m b( i, j ) = a( i, j ) end do end do else do j = 1, n do i = 1, m b( i, j ) = a( i, j ) end do end do end if returnend subroutine dlacpy
As may be observed, by removing column restrictions and moving away from the F77 convention of writing specifiers in ALL CAPS, modern Fortran code is more visibly consistent and thus more readable.
Labeled control structures
Another common practice in LAPACK routines is the use of labeled control structures. For example, consider the following code snippet in which the label 10 must match a corresponding CONTINUE.
DO 10 I = 1, 10 PRINT *, I 10 CONTINUE
Fortran 90 obviated the need for this practice and improved code readability by allowing one to use end do to end a do loop. This change is shown in the free form version of dlacpy provided above.
Assumed-size arrays
To allow flexibility in handling arrays of varying sizes, LAPACK routines commonly operate on arrays having an assumed-size. In the dlacpy routine above, the input matrix A is declared to be a two-dimensional array having an assumed-size according to the expression A(LDA, *). This expression declares that A has LDA number of rows and uses * as a placeholder to indicate that the size of the second dimension is determined by the calling program.
One consequence of using assumed-size arrays is that compilers are unable to perform bounds checking on the unspecified dimension. Thus, current best practice is to use explicit interfaces and assumed-shape arrays (e.g., A(LDA,:)) in order to prevent out-of-bounds memory access. This stated, the use of assumed-shape arrays can be problematic when needing to pass sub-matrices to other functions, as doing so requires slicing which often results in compilers creating internal copies of array data.
Migrating to Fortran 95
Needless to say, it took me a while to adjust to LAPACK conventions and adopt a LAPACK mindset. However, being something of a purist, if I was going to be porting over routines anyway, I at least wanted to bring those routines I did manage to port into a more modern age in hopes of improving code readability and future maintenance. So, after discussing things with stdlib maintainers, I settled on migrating routines to Fortran 95, which, while not the latest and greatest Fortran version, seemed to strike the right balance between maintaining the look-and-feel of the original implementations, ensuring (good enough) backward compatibility, and taking advantage of newer syntactical features.
Test Coverage
One of the problems with pursuing a bottom-up approach to adding LAPACK support is that explicit unit tests for lower-level utility routines are often non-existent in LAPACK. LAPACK's test suite largely employs a hierarchical testing philosophy in which testing higher-level routines is assumed to ensure that their dependent lower-level routines are functioning correctly as part of an overall workflow. While one can argue that focusing on integration testing over unit testing for lower-level routines is reasonable, as adding tests for every routine could potentially increase the maintenance burden and complexity of LAPACK's testing framework, it means that we couldn't readily rely on prior art for unit testing and would have to come up with comprehensive standalone unit tests for each lower-level routine on our own.
Documentation
Along a similar vein to test coverage, outside of LAPACK itself, finding real-world documented examples showcasing the use of lower-level routines was challenging. While LAPACK routines are consistently preceded by a documentation comment providing descriptions of input arguments and possible return values, without code examples, visualizing and grokking expected input and output values can be challenging, especially when dealing with specialized matrices. And while neither the absence of unit tests nor documented examples is the end of the world, it meant that adding LAPACK support to stdlib would be more of a slog than I expected. Writing benchmarks, tests, examples, and documentation was simply going to require more time and effort, potentially limiting the number of routines I could implement.
Memory layouts
When storing matrix elements in linear memory, one has two choices: either store columns contiguously or rows contiguously (see Figure 2). The former memory layout is referred to as column-major order and the latter as row-major order.
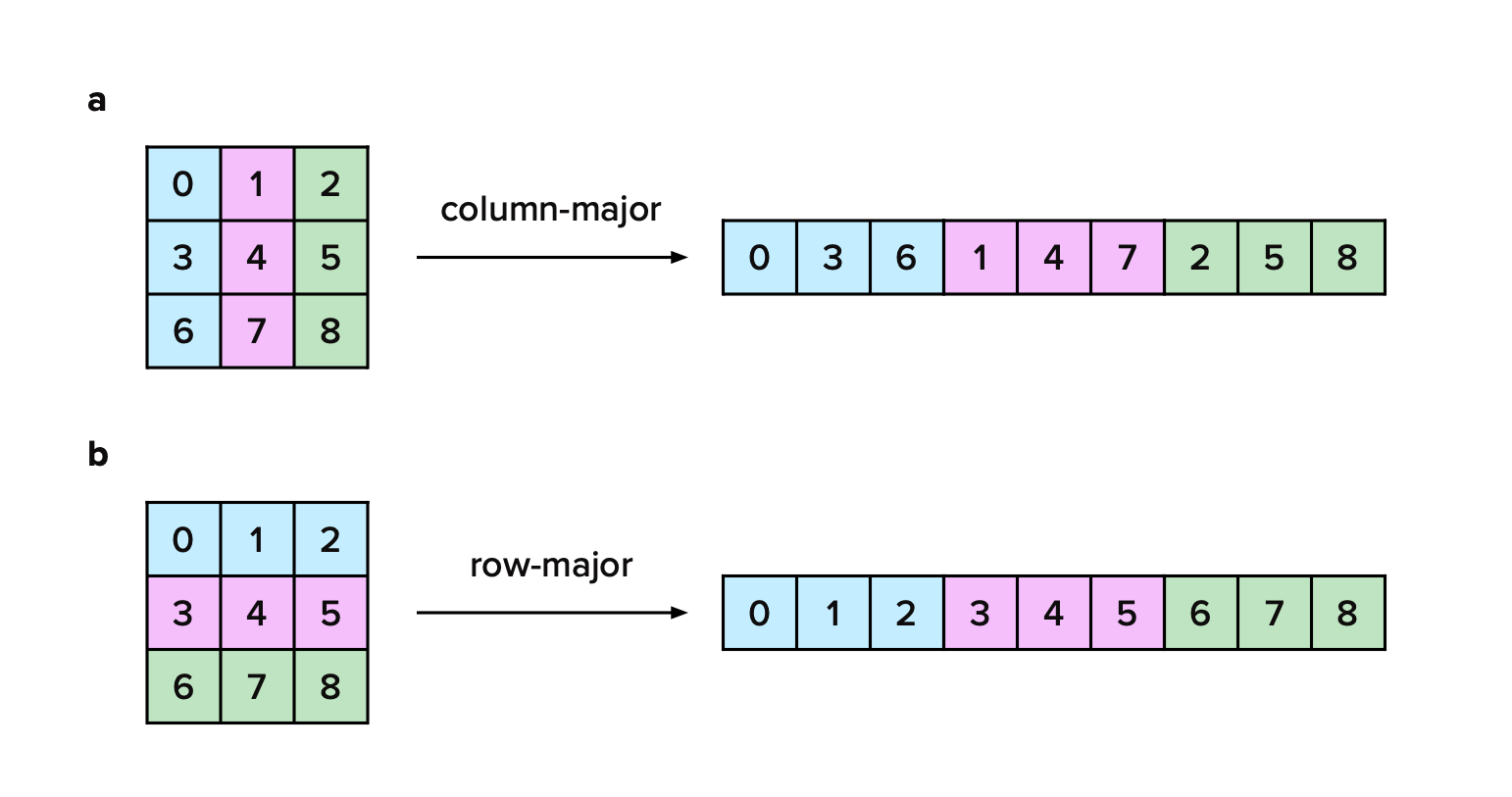
Figure 2: Schematic demonstrating storing matrix elements in linear memory in either (a) column-major (Fortran-style) or (b) row-major (C-style) order. The choice of which layout to use is largely a matter of convention.
The choice of which layout to use is largely a matter of convention. For example, Fortran stores elements in column-major order, and C stores elements in row-major order. Higher-level libraries, such as NumPy and stdlib, support both column- and row-major orders, allowing you to configure the layout of a multi-dimensional array during array creation.
import asarray from '@stdlib/ndarray-array';// Create a row-major array:const x = asarray([1.0, 2.0, 3.0, 4.0], { 'shape': [2, 2], 'order': 'row-major'});// Create a column-major array:const y = asarray([1.0, 3.0, 2.0, 4.0], { 'shape': [2, 2], 'order': 'column-major'});
While neither memory layout is inherently better than the other, arranging data to ensure sequential access in accordance with the conventions of the underlying storage model is critical in ensuring optimal performance. Modern CPUs are able to process sequential data more efficiently than non-sequential data, which is primarily due to CPU caching which, in turn, exploits spatial locality of reference.
To demonstrate the performance impact of sequential vs non-sequential element access, consider the following function which copies all the elements from an MxN matrix A to another MxN matrix B and which does so assuming that matrix elements are stored in column-major order.
/*** Copies elements from `A` to `B`.** @param {integer} M - number of rows* @param {integer} N - number of columns* @param {Array} A - source matrix* @param {integer} strideA1 - index increment to move to the next element in a column* @param {integer} strideA2 - index increment to move to the next element in a row* @param {integer} offsetA - index of the first indexed element in `A`* @param {Array} B - source matrix* @param {integer} strideB1 - index increment to move to the next element in a column* @param {integer} strideB2 - index increment to move to the next element in a row* @param {integer} offsetB - index of the first indexed element in `B`*/function copy(M, N, A, strideA1, strideA2, offsetA, B, strideB1, strideB2, offsetB) { // Initialize loop bounds: const S0 = M; const S1 = N; // For column-major matrices, the first dimension has the fastest changing index. // Compute "pointer" increments accordingly: const da0 = strideA1; // pointer increment for innermost loop const da1 = strideA2 - (S0*strideA1); // pointer increment for outermost loop const db0 = strideB1; const db1 = strideB2 - (S0*strideB1); // Initialize "pointers" to the first indexed elements in the respective arrays: let ia = offsetA; let ib = offsetB; // Iterate over matrix dimensions: for (let i1 = 0; i1 < S1; i1++) { for (let i0 = 0; i0 < S0; i0++) { B[ib] = A[ia]; ia += da0; ib += db0; } ia += da1; ib += db1; }}
Let A and B be the following 3x2 matrices:
When both A and B are stored in column-major order, we can call the copy routine as follows:
const A = [1, 3, 5, 2, 4, 6];const B = [0, 0, 0, 0, 0, 0];copy(3, 2, A, 1, 3, 0, B, 1, 3, 0);
If, however, A and B are both stored in row-major order, the call signature changes to
const A = [1, 2, 3, 4, 5, 6];const B = [0, 0, 0, 0, 0, 0];copy(3, 2, A, 2, 1, 0, B, 2, 1, 0);
Notice that, in the latter scenario, we fail to access elements in sequential order within the innermost loop, as da0 is 2 and da1 is -5 and similarly for db0 and db1. Instead, the array index "pointers" repeatedly skip ahead before returning to earlier elements in linear memory, with ia = {0, 2, 4, 1, 3, 5} and ib the same. In Figure 3, we show the performance impact of non-sequential access.
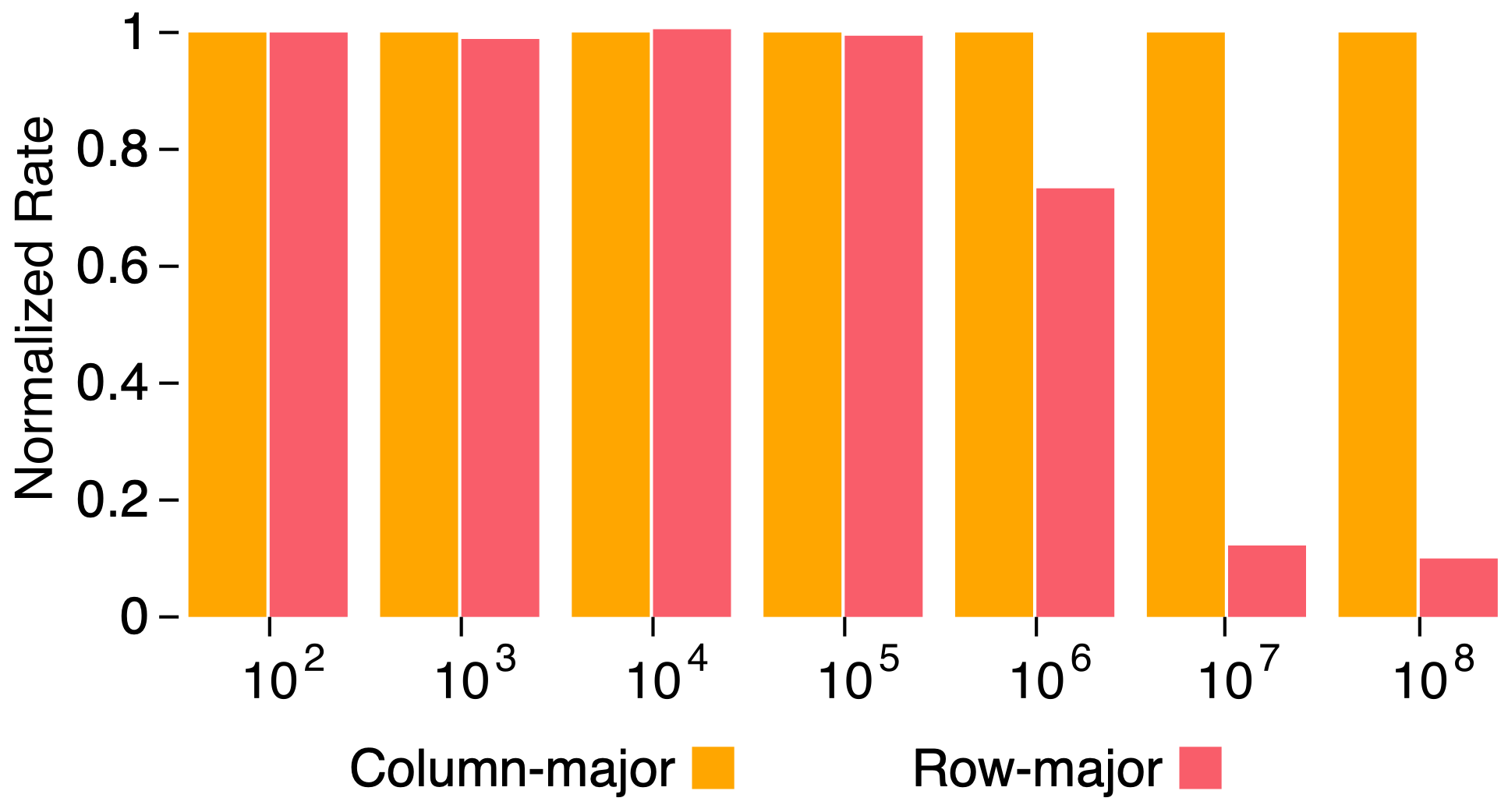
Figure 3: Performance comparison when providing square column-major versus row-major matrices to copy when copy assumes sequential element access according to column-major order. The x-axis enumerates increasing matrix sizes (i.e., number of elements). All rates are normalized relative to column-major results for a corresponding matrix size.
From the figure, we may observe that column- and row-major performance is roughly equivalent until we operate on square matrices having more than 1e5 elements (M = N = ~316). For 1e6 elements (M = N = ~1000), providing a row-major matrix to copy results in a greater than 25% performance decrease. For 1e7 elements (M = N = ~3160), we observe a greater than 85% performance decrease. The significant performance impact may be attributed to decreased locality of reference when operating on row-major matrices having large row sizes.
Given that it is written in Fortran, LAPACK assumes column-major access order and implements its algorithms accordingly. This presents issues for libraries, such as stdlib, which not only support row-major order, but make it their default memory layout. Were we to simply port LAPACK's Fortran implementations to JavaScript, users providing row-major matrices would experience adverse performance impacts stemming from non-sequential access.
To mitigate adverse performance impacts, we borrowed an idea from BLIS, a BLAS-like library supporting both row- and column-major memory layouts in BLAS routines, and decided to create modified LAPACK implementations when porting routines from Fortran to JavaScript and C that explicitly accommodate both column- and row-major memory layouts through separate stride parameters for each dimension. For some implementations, such as dlacpy, which is similar to the copy function defined above, incorporating separate and independent strides is straightforward, often involving stride tricks and loop interchange, but, for others, the modifications turned out to be much less straightforward due to specialized matrix handling, varying access patterns, and combinatorial parameterization.
ndarrays
LAPACK routines primarily operate on matrices stored in linear memory and whose elements are accessed according to specified dimensions and the stride of the leading (i.e., first) dimension. Dimensions specify the number of elements in each row and column, respectively. The stride specifies how many elements in linear memory must be skipped in order to access the next element of a row. LAPACK assumes that elements belonging to the same column are always contiguous (i.e., adjacent in linear memory). Figure 4 provides a visual representation of LAPACK conventions (specifically, schematics (a) and (b)).
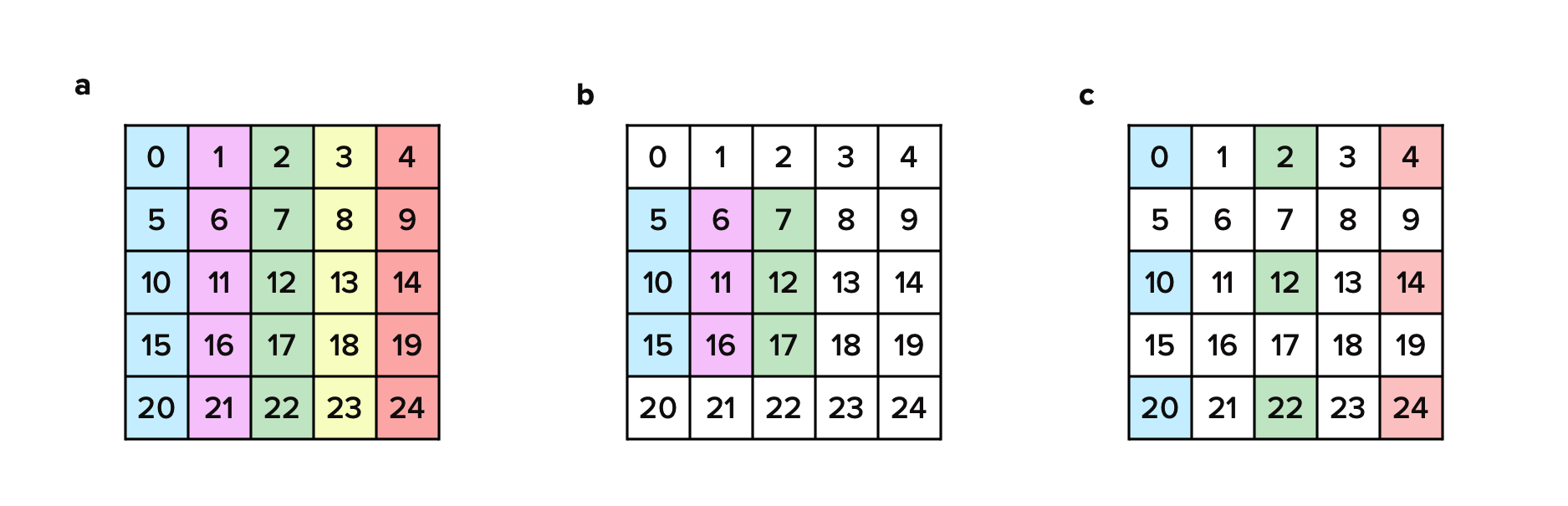
Figure 4: Schematics illustrating the generalization of LAPACK strided array conventions to non-contiguous strided arrays. a) A 5-by-5 contiguous matrix stored in column-major order. b) A 3-by-3 non-contiguous sub-matrix stored in column-major order. Sub-matrices can be operated on in LAPACK by providing a pointer to the first indexed element and specifying the stride of the leading (i.e., first) dimension. In this case, the stride of leading dimension is five, even though there are only three elements per column, due to the non-contiguity of sub-matrix elements in linear memory when stored as part of a larger matrix. In LAPACK, the stride of the trailing (i.e., second) dimension is always assumed to be unity. c) A 3-by-3 non-contiguous sub-matrix stored in column-major order having non-unit strides and generalizing LAPACK stride conventions to both leading and trailing dimensions. This generalization underpins stdlib's multi-dimensional arrays (also referred to as "ndarrays").
Libraries, such as NumPy and stdlib, generalize LAPACK's strided array conventions to support
- non-unit strides in the last dimension (see Figure 4 (c)). LAPACK assumes that the last dimension of a matrix always has unit stride (i.e., elements within a column are stored contiguously in linear memory).
- negative strides for any dimension. LAPACK requires that the stride of a leading matrix dimension be positive.
- multi-dimensional arrays having more than two dimensions. LAPACK only explicitly supports strided vectors and (sub)matrices.
Support for non-unit strides in the last dimension ensures support for O(1) creation of non-contiguous views of linear memory without requiring explicit data movement. These views are often called "slices". As an example, consider the following code snippet which creates such views using APIs provided by stdlib.
import linspace from '@stdlib/array-linspace'import FancyArray from '@stdlib/ndarray-fancy';// Define a two-dimensional array similar to that shown in Figure 4 (a):const x = new FancyArray('float64', linspace(0, 24, 25), [5, 5], [5, 1], 0, 'row-major');// returns <FancyArray>// Create a sub-matrix view similar to that shown in Figure 4 (b):const v1 = x['1:4,:3'];// returns <FancyArray>// Create a sub-matrix view similar to that shown in Figure 4 (c):const v2 = x['::2,::2'];// returns <FancyArray>// Assert that all arrays share the same underlying memory buffer:const b1 = (v1.data.buffer === x.data.buffer);// returns trueconst b2 = (v2.data.buffer === x.data.buffer);// returns true
Without support for non-unit strides in the last dimension, returning a view from the expression x['::2,::2'] would not be possible, as one would need to copy selected elements to a new linear memory buffer in order to ensure contiguity.

Figure 5: Schematics illustrating the use of stride manipulation to create flipped and rotated views of matrix elements stored in linear memory. For all sub-schematics, strides are listed as [trailing_dimension, leading_dimension]. Implicit for each schematic is an "offset", which indicates the index of the first indexed element such that, for a matrix A, the element Aij is resolved according to i⋅strides[1] + j⋅strides[0] + offset. a) Given a 3-by-3 matrix stored in column-major order, one can manipulate the strides of the leading and trailing dimensions to create views in which matrix elements along one or more axes are accessed in reverse order. b) Using similar stride manipulation, one can create rotated views of matrix elements relative to their arrangement within linear memory.
Support for negative strides enables O(1) reversal and rotation of elements along one or more dimensions (see Figure 5). For example, to flip a matrix top-to-bottom and left-to-right, one need only negate the strides. Building on the previous code snippet, the following code snippet demonstrates reversing elements about one or more axes.
import linspace from '@stdlib/array-linspace'import FancyArray from '@stdlib/ndarray-fancy';// Define a two-dimensional array similar to that shown in Figure 5 (a):const x = new FancyArray('float64', linspace(0, 8, 9), [3, 3], [3, 1], 0, 'row-major');// Reverse elements along each row:const v1 = x['::-1,:'];// Reverse elements along each column:const v2 = x[':,::-1'];// Reverse elements along both columns and rows:const v3 = x['::-1,::-1'];// Assert that all arrays share the same underlying memory buffer:const b1 = (v1.data.buffer === x.data.buffer);// returns trueconst b2 = (v2.data.buffer === x.data.buffer);// returns trueconst b3 = (v3.data.buffer === x.data.buffer);// returns true
Implicit in the discussion of negative strides is the need for an "offset" parameter which indicates the index of the first indexed element in linear memory. For a strided multi-dimensional array A and a list of strides s, the index corresponding to element Aij⋅⋅⋅n can be resolved according to the equation
where N is the number of array dimensions and sk corresponds to kth stride.
In BLAS and LAPACK routines supporting negative strides—something which is only supported when operating on strided vectors (e.g., see daxpy above)—the index offset is computed using logic similar to the following code snippet:
if (stride < 0) { offset = (1-M) * stride;} else { offset = 0;}
where M is the number of vector elements. This implicitly assumes that a provided data pointer points to the beginning of linear memory for a vector. In languages supporting pointers, such as C, in order to operate on a different region of linear memory, one typically adjusts a pointer using pointer arithmetic prior to function invocation, which is relatively cheap and straightforward, at least for the one-dimensional case.
For example, returning to c_daxpy as defined above, we can use pointer arithmetic to limit element access to five elements within linear memory beginning at the eleventh and sixteenth elements (note: zero-based indexing) of an input and output array, respectively, as shown in the following code snippet.
// Define data arrays:const double X[] = {...};double Y[] = {...};// Specify the indices of the elements which begin a desired memory region:const xoffset = 10;const yoffset = 15;// Limit the operation to only elements within the desired memory region:c_daxpy(5, 5.0, X+xoffset, 1, Y+yoffset, 1);
However, in JavaScript, which does not support explicit pointer arithmetic for binary buffers, one must explicitly instantiate new typed array objects having a desired byte offset. In the following code snippet, in order to achieve the same results as the C example above, we must resolve a typed array constructor, compute a new byte offset, compute a new typed array length, and create a new typed array instance.
/*** Returns a typed array view having the same data type as a provided input typed* array and starting at a specified index offset.** @param {TypedArray} x - input array* @param {integer} offset - starting index* @returns {TypedArray} typed array view*/function offsetView(x, offset) { return new x.constructor(x.buffer, x.byteOffset+(x.BYTES_PER_ELEMENT*offset), x.length-offset);}// ...const x = new Float64Array([...]);const y = new Float64Array([...]);// ...daxpy(5, 5.0, offsetView(x, 10), 1, offsetView(y, 15), 1);
For large array sizes, the cost of typed array instantiation is negligible compared to the time spent accessing and operating on individual array elements; however, for smaller array sizes, object instantiation can significantly impact performance.
Accordingly, in order to avoid adverse object instantiation performance impacts, stdlib decouples an ndarray's data buffer from the location of the buffer element corresponding to the beginning of an ndarray view. This allows the slice expressions x[2:,3:] and x[3:,1:] to return new ndarray views without needing to instantiate new buffer instances, as demonstrated in the following code snippet.
import linspace from '@stdlib/array-linspace'import FancyArray from '@stdlib/ndarray-fancy';const x = new FancyArray('float64', linspace(0, 24, 25), [5, 5], [5, 1], 0, 'row-major');const v1 = x['2:,3:'];const v2 = x['3:,1:'];// Assert that all arrays share the same typed array data instance:const b1 = (v1.data === x.data);// returns trueconst b2 = (v2.data === x.data);// returns true
As a consequence of decoupling a data buffer from the beginning of an ndarray view, we similarly sought to avoid having to instantiate new typed array instances when calling into LAPACK routines with ndarray data. This meant creating modified LAPACK API signatures supporting explicit offset parameters for all strided vectors and matrices.
For simplicity, let's return to the JavaScript implementation of daxpy, which was previously defined above.
function daxpy(N, alpha, X, strideX, Y, strideY) { let ix; let iy; let i; if (N <= 0) { return; } if (alpha === 0.0) { return; } if (strideX < 0) { ix = (1-N) * strideX; } else { ix = 0; } if (strideY < 0) { iy = (1-N) * strideY; } else { iy = 0; } for (i = 0; i < N; i++) { Y[iy] += alpha * X[ix]; ix += strideX; iy += strideY; } return;}
As demonstrated in the following code snippet, we can modify the above signature and implementation such that the responsibility for resolving the first indexed element is shifted to the API consumer.
function daxpy_ndarray(N, alpha, X, strideX, offsetX, Y, strideY, offsetY) { let ix; let iy; let i; if (N <= 0) { return; } if (alpha === 0.0) { return; } ix = offsetX; iy = offsetY; for (i = 0; i < N; i++) { Y[iy] += alpha * X[ix]; ix += strideX; iy += strideY; } return;}
For ndarrays, resolution happens during ndarray instantiation, making the invocation of daxpy_ndarray with ndarray data a straightforward passing of associated ndarray meta data. This is demonstrated in the following code snippet.
import linspace from '@stdlib/array-linspace'import FancyArray from '@stdlib/ndarray-fancy';// Create two ndarrays:const x = new FancyArray('float64', linspace(0, 24, 25), [5, 5], [5, 1], 0, 'row-major');const y = new FancyArray('float64', linspace(0, 24, 25), [5, 5], [5, 1], 0, 'row-major');// Create a view of `x` corresponding to every other element in the 3rd row:const v1 = x['2,1::2'];// Create a view of `y` corresponding to every other element in the 3rd column:const v2 = y['1::2,2'];// Operate on the vectors:daxpy_ndarray(v1.length, 5.0, v1.data, v1.strides[0], v1.offset, v2.data, v2.strides[0], v2.offset);
Similar to BLIS, we saw value in both conventional LAPACK API signatures (e.g., for backward compatibility) and modified API signatures (e.g., for minimizing adverse performance impacts), and thus, we settled on a plan to provide both conventional and modified APIs for each LAPACK routine. To minimize code duplication, we aimed to implement a common lower-level "base" implementation which could then be wrapped by higher-level APIs. While the changes for the BLAS routine daxpy shown above may appear relatively straightforward, the transformation of a conventional LAPACK routine and its expected behavior to a generalized implementation was often much less so.
dlaswp
Enough with the challenges! What did a final product look like?!
Let's come full circle and bring this back to dlaswp, a LAPACK routine for performing a series of row interchanges on an input matrix according to a list of pivot indices. The following code snippet shows the reference LAPACK Fortran implementation.
SUBROUTINE dlaswp( N, A, LDA, K1, K2, IPIV, INCX )** -- LAPACK auxiliary routine --* -- LAPACK is a software package provided by Univ. of Tennessee, --* -- Univ. of California Berkeley, Univ. of Colorado Denver and NAG Ltd..--** .. Scalar Arguments .. INTEGER INCX, K1, K2, LDA, N* ..* .. Array Arguments .. INTEGER IPIV( * ) DOUBLE PRECISION A( LDA, * )* ..** =====================================================================** .. Local Scalars .. INTEGER I, I1, I2, INC, IP, IX, IX0, J, K, N32 DOUBLE PRECISION TEMP* ..* .. Executable Statements ..** Interchange row I with row IPIV(K1+(I-K1)*abs(INCX)) for each of rows* K1 through K2.* IF( incx.GT.0 ) THEN ix0 = k1 i1 = k1 i2 = k2 inc = 1 ELSE IF( incx.LT.0 ) THEN ix0 = k1 + ( k1-k2 )*incx i1 = k2 i2 = k1 inc = -1 ELSE RETURN END IF* n32 = ( n / 32 )*32 IF( n32.NE.0 ) THEN DO 30 j = 1, n32, 32 ix = ix0 DO 20 i = i1, i2, inc ip = ipiv( ix ) IF( ip.NE.i ) THEN DO 10 k = j, j + 31 temp = a( i, k ) a( i, k ) = a( ip, k ) a( ip, k ) = temp 10 CONTINUE END IF ix = ix + incx 20 CONTINUE 30 CONTINUE END IF IF( n32.NE.n ) THEN n32 = n32 + 1 ix = ix0 DO 50 i = i1, i2, inc ip = ipiv( ix ) IF( ip.NE.i ) THEN DO 40 k = n32, n temp = a( i, k ) a( i, k ) = a( ip, k ) a( ip, k ) = temp 40 CONTINUE END IF ix = ix + incx 50 CONTINUE END IF* RETURN** End of DLASWP* END
To facilitate interfacing with the Fortran implementation from C, LAPACK provides a two-level C interface called LAPACKE, which wraps Fortran implementations and makes accommodations for both row- and column-major input and output matrices. The middle-level interface for dlaswp is shown in the following code snippet.
lapack_int LAPACKE_dlaswp_work( int matrix_layout, lapack_int n, double* a, lapack_int lda, lapack_int k1, lapack_int k2, const lapack_int* ipiv, lapack_int incx ){ lapack_int info = 0; if( matrix_layout == LAPACK_COL_MAJOR ) { /* Call LAPACK function and adjust info */ LAPACK_dlaswp( &n, a, &lda, &k1, &k2, ipiv, &incx ); if( info < 0 ) { info = info - 1; } } else if( matrix_layout == LAPACK_ROW_MAJOR ) { lapack_int lda_t = MAX(1,k2); lapack_int i; for( i = k1; i <= k2; i++ ) { lda_t = MAX( lda_t, ipiv[k1 + ( i - k1 ) * ABS( incx ) - 1] ); } double* a_t = NULL; /* Check leading dimension(s) */ if( lda < n ) { info = -4; LAPACKE_xerbla( "LAPACKE_dlaswp_work", info ); return info; } /* Allocate memory for temporary array(s) */ a_t = (double*)LAPACKE_malloc( sizeof(double) * lda_t * MAX(1,n) ); if( a_t == NULL ) { info = LAPACK_TRANSPOSE_MEMORY_ERROR; goto exit_level_0; } /* Transpose input matrices */ LAPACKE_dge_trans( matrix_layout, lda_t, n, a, lda, a_t, lda_t ); /* Call LAPACK function and adjust info */ LAPACK_dlaswp( &n, a_t, &lda_t, &k1, &k2, ipiv, &incx ); info = 0; /* LAPACK call is ok! */ /* Transpose output matrices */ LAPACKE_dge_trans( LAPACK_COL_MAJOR, lda_t, n, a_t, lda_t, a, lda ); /* Release memory and exit */ LAPACKE_free( a_t );exit_level_0: if( info == LAPACK_TRANSPOSE_MEMORY_ERROR ) { LAPACKE_xerbla( "LAPACKE_dlaswp_work", info ); } } else { info = -1; LAPACKE_xerbla( "LAPACKE_dlaswp_work", info ); } return info;}
When called with a column-major matrix a, the wrapper LAPACKE_dlaswp_work simply passes along provided arguments to the Fortran implementation. However, when called with a row-major matrix a, the wrapper must allocate memory, explicitly transpose and copy a to a temporary matrix a_t, recompute the stride of the leading dimension, invoke dlaswp with a_t, transpose and copy the results stored in a_t to a, and finally free allocated memory. That is a fair amount of work and is common across most LAPACK routines.
The following code snippet shows the reference LAPACK implementation ported to JavaScript, with support for leading and trailing dimension strides, index offsets, and a strided vector containing pivot indices.
// File: base.js// ...const BLOCK_SIZE = 32;// ...function base(N, A, strideA1, strideA2, offsetA, k1, k2, inck, IPIV, strideIPIV, offsetIPIV) { let nrows; let n32; let tmp; let row; let ia1; let ia2; let ip; let o; // Compute the number of rows to be interchanged: if (inck > 0) { nrows = k2 - k1; } else { nrows = k1 - k2; } nrows += 1; // If the order is row-major, we can delegate to the Level 1 routine `dswap` for interchanging rows... if (isRowMajor([strideA1, strideA2])) { ip = offsetIPIV; for (let i = 0, k = k1; i < nrows; i++, k += inck) { row = IPIV[ip]; if (row !== k) { dswap(N, A, strideA2, offsetA+(k*strideA1), A, strideA2, offsetA+(row*strideA1)); } ip += strideIPIV; } return A; } // If the order is column-major, we need to use loop tiling to ensure efficient cache access when accessing matrix elements... n32 = floor(N/BLOCK_SIZE) * BLOCK_SIZE; if (n32 !== 0) { for (let j = 0; j < n32; j += BLOCK_SIZE) { ip = offsetIPIV; for (let i = 0, k = k1; i < nrows; i++, k += inck) { row = IPIV[ip]; if (row !== k) { ia1 = offsetA + (k*strideA1); ia2 = offsetA + (row*strideA1); for (let n = j; n < j+BLOCK_SIZE; n++) { o = n * strideA2; tmp = A[ia1+o]; A[ia1+o] = A[ia2+o]; A[ia2+o] = tmp; } } ip += strideIPIV; } } } if (n32 !== N) { ip = offsetIPIV; for (let i = 0, k = k1; i < nrows; i++, k += inck) { row = IPIV[ ip ]; if (row !== k) { ia1 = offsetA + (k*strideA1); ia2 = offsetA + (row*strideA1); for (let n = n32; n < N; n++) { o = n * strideA2; tmp = A[ia1+o]; A[ia1+o] = A[ia2+o]; A[ia2+o] = tmp; } } ip += strideIPIV; } } return A;}
To provide an API having consistent behavior with conventional LAPACK, I then wrapped the above implementation and adapted input arguments to the "base" implementation, as shown in the following code snippet.
// File: dlaswp.js// ...const base = require('./base.js');// ...function dlaswp(order, N, A, LDA, k1, k2, IPIV, incx) { let tmp; let inc; let sa1; let sa2; let io; if (!isLayout(order)) { throw new TypeError(format('invalid argument. First argument must be a valid order. Value: `%s`.', order)); } if (order === 'row-major' && LDA < max(1, N)) { throw new RangeError(format('invalid argument. Fourth argument must be greater than or equal to max(1,%d). Value: `%d`.', N, LDA)); } if (incx > 0) { inc = 1; io = k1; } else if (incx < 0) { inc = -1; io = k1 + ((k1-k2) * incx); tmp = k1; k1 = k2; k2 = tmp; } else { return A; } if (order === 'column-major') { sa1 = 1; sa2 = LDA; } else { // order === 'row-major' sa1 = LDA; sa2 = 1; } return base(N, A, sa1, sa2, 0, k1, k2, inc, IPIV, incx, io);}
I subsequently wrote a separate but similar wrapper which provides an API mapping more directly to stdlib's multi-dimensional arrays and which performs some special handling when the direction in which to apply pivots is negative, as shown in the following code snippet.
// File: ndarray.jsconst base = require('./base.js');// ...function dlaswp_ndarray(N, A, strideA1, strideA2, offsetA, k1, k2, inck, IPIV, strideIPIV, offsetIPIV) { let tmp; if (inck < 0) { offsetIPIV += k2 * strideIPIV; strideIPIV *= -1; tmp = k1; k1 = k2; k2 = tmp; inck = -1; } else { offsetIPIV += k1 * strideIPIV; inck = 1; } return base(N, A, strideA1, strideA2, offsetA, k1, k2, inck, IPIV, strideIPIV, offsetIPIV);}
A few points to note:
- In contrast to the conventional LAPACKE API, the
matrix_layout(order) parameter is not necessary in thedlaswp_ndarrayandbaseAPIs, as the order can be inferred from the provided strides. - In contrast to the conventional LAPACKE API, when an input matrix is row-major, we don't need to copy data to temporary workspace arrays, thus reducing unnecessary memory allocation.
- In contrast to libraries, such as NumPy and SciPy, which interface with BLAS and LAPACK directly, when calling LAPACK routines in stdlib, we don't need to copy non-contiguous multi-dimensional data to and from temporary workspace arrays before and after invocation, respectively. Except when interfacing with hardware-optimized BLAS and LAPACK, the approach pursued during this internship helps minimize data movement and ensures performance in resource constrained browser applications.
For server-side applications hoping to leverage hardware-optimized libraries, such as OpenBLAS, we provide separate wrappers which adapt generalized signature arguments to their optimized API equivalents. In this context, at least for sufficiently large arrays, creating temporary copies can be worth the overhead.
Current status and next steps
Despite the challenges, unforeseen setbacks, and multiple design iterations, I am happy to report that, in addition to dlaswp above, I was able to open 35 PRs adding support for various LAPACK routines and associated utilities, and I co-authored a blog post with Athan Reines on "How to Call Fortran Routines from JavaScript Using Node.js". Obviously not quite 1,700 routines, but a good start! :)
Nevertheless, the future is bright, and we are quite excited about this work. There's still plenty of room for improvement and additional research and development. In particular, we're keen to
- explore tooling and automation.
- address build issues when resolving the source files of Fortran dependencies spread across multiple stdlib packages.
- roll out C and Fortran implementations and native bindings for stdlib's existing LAPACK packages.
- continue growing stdlib's library of modular LAPACK routines.
- identify additional areas for performance optimization.
While the internship has ended, my plan is to continue adding packages and pushing this effort along. Given the immense potential and LAPACK's fundamental importance, we'd love to see this initiative of bringing LAPACK to the web continue to grow, so, if you are interested in helping out and even sponsoring development, please don't hesitate to reach out! The folks at Quansight would be more than happy to chat.
Acknowledgments
And with that, I would like to thank Quansight and Athan Reines for providing me with this opportunity. I feel incredibly fortunate to have learned so much. Being an intern at Quansight was long a dream of mine, and I am very grateful to have fulfilled it. I want to extend a special thanks to Melissa Mendonça, who is an amazing mentor and all around wonderful person; thank you for investing so much time in us! And thank you to everyone else at Quansight for helping me out in ways both big and small along the way.
Cheers!